About me

Foto saya
simple, baik, sopan, enak bercanda, suka tantangan/petualang, yg paling penting jujur.

Blog

29 Okt 2011

Cara Menghitun Perkalian

Diposting oleh maman matematika di 10.24

Perkalian adalah operasi matematika penskalaan satu bilangan dengan bilangan lain. Operasi ini adalah salah satu dari empat operasi dasar di dalam aritmetika dasar (yang lainnya adalah perjumlahan, perkurangan, dan perbagian).
Perkalian terdefinisi untuk seluruh bilangan di dalam suku-suku perjumlahan yang diulang-ulang; misalnya, 3 dikali 4 (seringkali dibaca "3 kali 4") dapat dihitung dengan menjumlahkan 3 salinan dari 4 bersama-sama:
3 \times 4 = 4 + 4 + 4 = 12.\!\,
Perkalian bilangan rasional (pecahan) dan bilangan real didefinisi oleh perumumam gagasan dasar ini.
Perkalian dapat juga digambarkan sebagai pencacahan objek yang disusun di dalam persegi panjang (untuk semua bilangan) atau seperti halnya penentuan luas persegi panjang yang sisi-sisinya memberikan panjang (untuk bilangan secara umum). Balikan dari perkalian adalah perbagian: ketika 3 kali 4 sama dengan 12, maka 12 dibagi 3 sama dengan 4.
Perkalian diperumum ke jenis bilangan lain (misalnya bilangan kompleks) dan ke konstruksi yang lebih abstrak seperti matriks.
Catatan
Matematika merupakan ilmu dasar yang mendasari semua penerapan dalam kehidupan nyata. Contoh penerapan nyata adalah dalam bidang medis. Ketika kita mendapatkan obat dari dokter 3x1 berarti 3 kali dalam sehari (pagi, siang, malam) masing-masing 1 (pil). Bukan sebaliknya, 1 kali dalam sehari 3 (pil).
Hal ini perlu diperhatikan karena prosesnya sangat berbeda antara 3x2 dan 2x3. Seringkali kita berfokus pada hasilnya yang sama-sama 6. Penjelasan dalam bidang medis akan sangat jelas: 3x2 berarti 3 kali dalam sehari masing-masing 2 (pil) sedangkan 2x3 berarti 2 kali dalam sehari masing-masing 3 (pil). Dengan demikian, penjabaran dalam penjumlahan : 3x2 = 2 + 2 + 2; sedangkan 2x3 = 3 + 3.
Penekanan proses ini merupakan kewajiban bagi pengajar dan penulis buku tentang perkalian. Proses ini akan konsisten untuk diterapkan dalam bidang selain medis. Contohnya dalam ekonomi, 4 anak membeli 1 buku @ Rp. 1.000. Penulisan dalam bentuk perkalian adalah : 4 x Rp. 1.000. Penulisan dalam bentuk penjumlahan adalah : Rp. 1.000 + Rp. 1.000 + Rp. 1.000 + Rp. 1.000.
Perkalian vektor adalah operasi perkalian dengan dua operand (obyek yang dikalikan) berupa vektor. Terdapat tiga macam perkalian vektor, yaitu perkalian titik (dot product), perkalian silang (cross product) dan perkalian langsung (direct product).
Perkalian titik
Perkalian titik dua buah vektor akan menghasilkan sebuah skalar. Jenis perkalian ini bersifat komutatif.
\! \vec{A} \cdot \vec{B} = (a_x \hat{i} + a_y \hat{j} + a_z \hat{k}) \cdot (b_x \hat{i} + b_y \hat{j} + b_z \hat{k})
= a_x b_x + a_y b_y + a_z b_z \!
Untuk vektor satuan terdapat hubungan-hubungan yang khusus dalam operasi perkalian titik, yang merupakan sifat-sifat yang digunakan dalam perkalian titik, yaitu
\hat{i} \cdot \hat{i} = 1
\hat{j} \cdot \hat{j} = 1
\hat{k} \cdot \hat{k} = 1
dan
\hat{i} \cdot \hat{j} = \hat{j} \cdot \hat{i} = 0
\hat{j} \cdot \hat{k} = \hat{k} \cdot \hat{j} = 0
\hat{k} \cdot \hat{i} = \hat{i} \cdot \hat{k} = 0
Atau dapat pula dituliskan dengan menggunakan notasi delta Kronecker \!\delta_{mn}, yaitu
\hat{m} \cdot \hat{n} = \delta_{mn}
Perkalian silang
Hasil suatu perkalian silang dua buah vektor adalah juga sebuah vektor. Perkalian silang bersifat tidak komutatif.
\vec{A} \times \vec{B} = (a_x \hat{i} + a_y \hat{j} + a_z \hat{k}) \times (b_x \hat{i} + b_y \hat{j} + b_z \hat{k})
= (a_y b_z - a_z b_y) \hat{i} + (a_z b_x - a_x b_z) \hat{j} + (a_x b_y - a_y b_x) \hat{k}
Untuk vektor-vektor satuan terdapat pula hubungan yang mendasari operasi perkalian silang, yaitu
\hat{i} \times \hat{j} = \hat{k}
\hat{j} \times \hat{k} = \hat{i}
\hat{k} \times \hat{i} = \hat{j}
dan
\hat{j} \times \hat{i} = - \hat{k}
\hat{k} \times \hat{j} = - \hat{i}
\hat{i} \times \hat{k} = - \hat{j}.
Perkalian langsung
Hasil perkalian langsung dua buah vektor adalah sebuah tensor atau matriks. Perkalian ini tidak bersifat komutatif.
\vec{A} \vec{B} = (a_x \hat{i} + a_y \hat{j} + a_z \hat{k}) (b_x \hat{i} + b_y \hat{j} + b_z \hat{k})
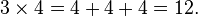
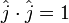
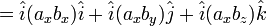
= \hat{i} (a_x b_x) \hat{i} + \hat{i} (a_x b_y) \hat{j} + \hat{i} (a_x b_z) \hat{k}
+ \hat{j} (a_y b_x) \hat{i} + \hat{j} (a_y b_y) \hat{j} + \hat{j} (a_y b_z) \hat{k}
+ \hat{k} (a_z b_x) \hat{i} + \hat{k} (a_z b_y) \hat{j} + \hat{k} (a_z b_z) \hat{k}
Perkalian langsung dua buah vektor satuan tidak memiliki hubungan yang khusus.
(\hat{a})(\hat{b}) = \hat{a} \hat{b}
\hat{a} \hat{b} \neq \hat{b} \hat{a}
Label:

0 komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)


Love Matematic Edited by Maman Suryaman © 2011